2960
|
2970
|
2980
|
2990
|
44999
|
45712
|
7136
|
6905
|
4080
|
8040
|
SEGUNDA SEMANA
división
|
Cociente
|
residuo
|
a. 385.68 7/ 5
|
48687
|
05
|
b. 333.600 / 3
|
77137
|
4
|
c. 569.685 / 8
|
71210
|
000
|
d. 292.126 /
6
|
111200
|
37
|
segundo periodo
Adición
|
Sustracción
|
||
908.201+
2.004
790.405
45.200
|
20.700+
2.321
119
130.885_
|
40.000-
19.076_
|
408.005-
289.874_
|
adición
|
sustracción
|
||
108.302+
1.024
90.206
5.800
|
50.300+
7.382
555
50.025
|
70.000-
43.196_
|
688.009-
209.273_
|
multiplicación
|
división
|
||
624.819
X 65_
|
981.418
X 759_
|
742.865 / 69
|
987.803 / 75
|
Decimos que un número es múltiplo de otro si le contiene un número entero de veces.
DOCENTE: FECHA: SEMANA No 1 Y 02, del 07 al 18 de septiembre NOMBRE ESTUDIANTE: _____________________________________
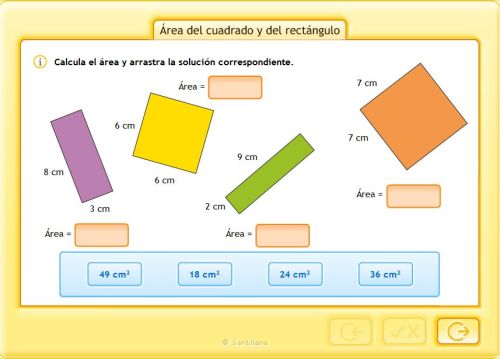
GRUPO:____ OBJETIVO.CALCULAR EL ÁREA O PERÍMETRO DE UNA FIGURA APRENDERÁS A CALCULAR EL PERÍMETRO O ÁREA DE UNA FIGURA
GEOMÉTRICA IDENTIFICADA EN CUALQUIER ESPACIO CON AYUDA DE TU FAMILIA LEE EL TEXTO Y RESPONDE LAS
ACTIVIDADES. EL PERÍMETRO Llamamos perímetro
de una figura geométrica plana a la longitud de su contorno. 2. El perímetro
de una figura geométrica siempre puede calcularse sumando la longitud de cada
uno de sus lados. Ejemplo ÁREAS DE FIGURAS PLANAS El área de una figura, es el número que indica la porción de
plano que ocupa. Se expresa en unidades de superficie. Área de figuras planas: Para hallar el área de
algunas figuras debes reconocer en ellas su base y su altura para luego aplicar
la fórmula dada. Área del rectángulo: El área
del rectángulo cualquiera se obtiene multiplicando la medida de la base por
la medida de la altura. Ejemplo Área del Cuadrado: Como el cuadrado es un
rectángulo en el que la base es igual a la altura, su área se calcula del
mismo modo que el área del rectángulo. Así, el área del cuadrado, que tiene 3
cm de lado, es: Área del
cuadrado = 3 cm x 3 cm = 9 cm2 ejemplo Actividad para entregar Actividad 1 Calcula el perímetro
y área de las siguientes figuras ·
Califica cada uno de los criterios. Encierra
en un círculo el número que corresponde a la nota de autoevaluación.
|
|||||||
ACTIVIDAD ACADÉMICA DEL ÁREA RECUPERACIONES MATEMATICA
DOCENTE:
FECHA: SEMANA No 02, del 14 al
18 de septiembre
NOMBRE ESTUDIANTE: _____________________________________
GRUPO:____
Realice correctamente las operaciones observe si es división
o multiplicación.
1. Escribe en forma de multiplicación: 4+4+4+4+4
2. ¿Qué haríamos para calcular el doble de un número?
a. Sumar dos
b. dividir por dos
c. multiplicar por dos
3. ¿Cuál de las respuestas NO es igual a 10?
a. 10x0
b. 2x5
c. 10x1
4. Eva quiere leer un cuento de treinta y seis páginas en
vacaciones si están duran cuatro semanas ¿cuántas páginas debe leer cada
semana?
5. Hemos cenado cinco amigos de una pizza que valía 30 PESOS
¿Cuánto hemos pagado cada uno de nosotros?
ACTIVIDAD ACADÉMICA DEL ÁREA MATEMÁTICAS
DOCENTE:
FECHA: SEMANA No
3 y 4 del 21 al 02 de octubre
NOMBRE ESTUDIANTE:
_____________________________________ GRUPO:____
CON AYUDA DE TU FAMILIA REALIZ A LOS TALLERES
OBJETIVO: Construir el proceso de composición factorial a partir de la
utilización de material concreto calculando el MCM a partir de la resolución de
problemas.
INTRUDUCCIÓN: para tener una idea clara de lo
que son los factores, a estos se le llaman factores o divisores de una
expresión algebraica, también las expresiones algebraicas que al multiplicando
entre ellos el producto de la expresión es original
AREA: MATEMATICAS.
TEMA: Descomposición de números primos y MCM
Qué
es el mínimo común múltiplo (mcm)?
El mínimo común múltiplo
(mcm) es el número positivo más pequeño que es múltiplo de dos o más números.
Para entender mejor esta
definición vamos a ver todos los términos.
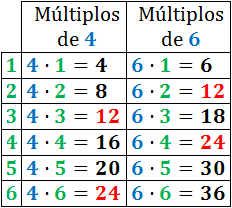
Múltiplo
Los múltiplos de un número
son los que obtienes cuando lo multiplicas por otros números.
Vamos a ver un ejemplo de
los múltiplos de 2 y de 3. Para calcular sus múltiplos hay que ir multiplicando
el 2 y el 3 por 1, por 2, por 3, etc.
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
Y así sucesivamente hasta
infinitos números.
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
y así sucesivamente hasta
infinitos números.
Múltiplo
Común
Un múltiplo común es un
número que es múltiplo a la vez de dos o más números, es decir, es un múltiplo común a esos números.
Siguiendo como ejemplos
anteriores vamos, a ver los múltiplos comunes de 2 y 3
Habrá que ver qué múltiplos tienen en
común el dos y el tres, que en la imagen figuran en verde, es decir, el 6, el
12 y el 18. Hay que tener en cuenta que
los múltiplos son infinitos y que nosotros solo hemos mostrados los primeros de
cada número.
Mínimo
común múltiplo
El mínimo común múltiplo es el número
más pequeño de los múltiplos comunes.
Siguiendo con el ejemplo anterior, si los
múltiplos comunes de 2 y de 3 eran 6, 12 y 18, el mínimo común múltiplo o mcm
es 6, ya que es el menor de los múltiplos comunes.
Cómo
calcular el mínimo común múltiplo (lee bien este método)
Se pueden utilizar dos métodos.
1. El primer método para calcular el mcm es el que hemos utilizado
antes, es decir, escribimos los primeros múltiplos de cada número, señalamos
los múltiplos que sean comunes y elegimos el múltiplo común más pequeño.
2. Ahora vamos a explicar el segundo método para calcular el mcm. Lo primero que
hay que hacer es descomponer en factores primos cada número. Después tendremos
que elegir los factores comunes y no comunes elevados al mayor exponente y por
último, tendremos que multiplicar los factores elegidos.
ver el video
ACTIVIDAD. PARA
ENTREGAR COPIAR EN EL CUADERNO.
1*¿Calcule el( MCM) en la tabla del
a. 6 y 4
b. 2 y 8
2*¿Usamos el (MCM) para resolver problemas?
3*¿Explique la formula para calcular el (MCM)?(
Lee el texto)
EVALUACIÓN.
·
Califica cada uno de los
criterios. Encierra en un círculo el número que corresponde a la nota de
autoevaluación.
|
Aprendí la
importancia del tema trabajado. |
1. 2. 3. 4. 5. |
|
Manifiesto
capacidad e interés para seguir instrucciones en el desarrollo de las
actividades. |
1. 2. 3. 4. 5. |
|
Soy responsable en cumplimiento de los compromisos
académicos. |
1.
2. 3. 4. 5. |
2+ TEMA: NUMEROS PRIMOS
En términos básicos son
todos aquellos números que tienen tan solo dos divisores: ellos mismos y
la unidad, es decir, el número 1.
Son todos los mayores a 1
siendo el primero el número 2 y el único de estos números par mientras que los
demás son llamados como “números primos impares”. EL 1 ES EL único número que
no es primo ni compuesto.
Qué
es un número primo
Un número primo puede
definirse como aquel número entero que es mayor de 0 y tiene 2 divisores,
el 1 y el mismo.
Cuáles
son los números primos
NÚMEROS PRIMOS DEL 1 AL 100
ACTIVIDAD: PARA ENTREGAR
COPIAR EN EL CUADERNO.
1*¿Escribe cuáles son los números primos?
2*¿Cuál es el número primo más pequeño?
3*¿Cuál de estos números son primos?
A* 12 B* 6
C* 9 D* 7
4*¿Cuál de estos números son compuestos
A*21 B*13 C* 2 D* 11
5*¿Qué número no es primo ni compuesto?
A*15
B*42 C* 18 D*1
·
EVALUACIÓN. Califica cada uno de los
criterios. Encierra en un círculo el número que corresponde a la nota de
autoevaluación.
|
Aprendí la
importancia del tema trabajado. |
1. 2. 3. 4. 5. |
|
Manifiesto
capacidad e interés para seguir instrucciones en el desarrollo de las
actividades. |
1. 2. 3. 4. 5. |
|
Soy responsable en cumplimiento de los compromisos
académicos. |
1.
2. 3. 4. 5. |
ACTIVIDAD ACADÉMICA DEL ÁREA matemática
DOCENTE:
FECHA: SEMANA No 05 – 06, del 13
al 23 de octubre
NOMBRE ESTUDIANTE: _____________________________________
GRUPO:____
OBJETIVO Identificar
relaciones de divisibilidad entre números naturales y reconocer si un número es
múltiplo o divisor de otro número dado y cuáles son los números compuestos.
INTRODUCCIÓN: Cabe mencionar que para poder trabajar y
entender las operaciones que se realizan dentro de estos dos temas es necesaria
la revisión de conceptos previos de la teoría de la divisibilidad, la teoría de
los números primos así como de los múltiplos y de los divisores los cuales nos permitirán realizar relaciones
entre ellos.
TEMA: MCD Y NÚMEROS COMPUESTOS.
|
*En compañía de tus padres o acudientes realiza las siguientes
actividades: Del millón de
amigos que tengo, los del grado cuarto son…¡lo máximo!
1.
Te reto a enviar un vídeo
entonando esta declamación El máximo común divisor o también denominado como MCD, es el
MAYOR de los DIVISORES COMUNES de dos o más números. Para entender
que es el MCD es importante definir
y aclarar los siguientes términos, veamos:
Máximo:
Es el número mayor, o
sea que elegimos el número más grande. Ejemplo: 1, 3…
è el
máximo es el 3 Común:
Es el número que se
repite en los divisores de dos o más números. Ejemplo: D3 =
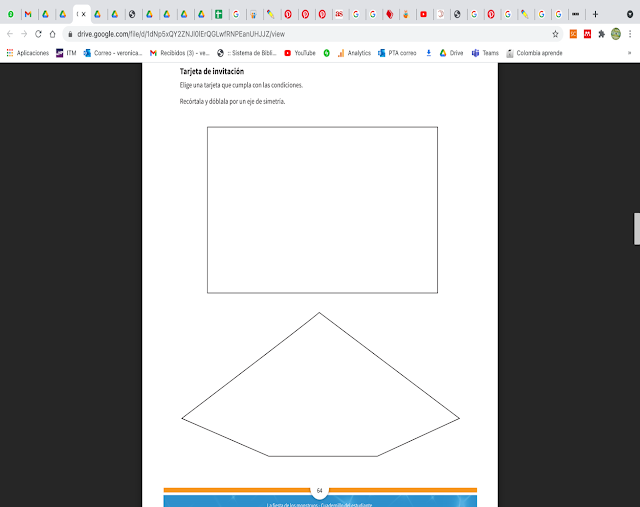
{1, 3} D6 = {1, 2, 3, 6} D9 = {1, 3, 9] è Para 3, 6 y 9 son comunes el 1 y el 3 v ¿Qué Aprendó? Actividades: para entregar y copiar en el cuaderno 1*Diseña una tarjeta para una persona especial y así poder llegar a tener un millón de amigos. Puedes entregar la tarjeta personalmente o tomar una foto y enviársela 2*, escríbelos en el cuaderno de Matemáticas y halla el MCD de 12 y 14 b. halla el mcd de 18 y 16 EVALUACIÓN. Ahora te propongo que
respondas las siguientes preguntas: Si sientes que has aprendido 1-¿Qué aprendiste?
Explícalo con tus propias palabras 2-¿Qué otras situaciones
pueden representar, de acuerdo al tema,
en tu entorno o vida diaria. Temas. 2°
NUMERO COMPUESTOS. Un número compuesto es el que posee más de dos
divisores. Es decir, aquel que se puede dividir por sí mismo, por la unidad y
por otros números. Un número compuesto es un número entero con más de dos
divisores integrales. Así todos los números enteros (excepto 0 y 1) son o primos o compuestos. Ejemplos: 12 = 2 · 2 · 3 72 = 2 · 4 · 9 144 = 2 · 6 · 12 ¿Qué Aprendó?ACTIVIDAD
PARA ENTREGAR 1* Seleccione solos los números que son
compuestos. ° 74----- °13____ °67____ °84____
2* En la tabla busca cuales son los números
primos y cuales son compuestos. ayudate con el tema anterior Evaluación Ahora te propongo que respondas las siguientes preguntas: Si sientes que has aprendido 1-¿Qué aprendiste?
Explícalo con tus propias palabras 2-¿Qué otras situaciones
pueden representar, de acuerdo al tema,
en tu entorno o vida diaria.
ACTIVIDAD ACADÉMICA DEL ÁREA MATEMATICA DOCENTE: FECHA: SEMANA No 07– 08, del 26 al 06 de noviembre NOMBRE ESTUDIANTE: _____________________________________ GRUPO:__ OBJETIVO: USAR TECNICA ELEMENTALES DE RECOGIDA DE DATOS PARA OBTENER INFORMACION SOBRE FENOMENOS COTIDIANOS; REPRESENTARLA EN FORMA GRAFICA Y NUMERICA Y FORMARSE UN JUICIO SOBRE LA MISMA. INTRODUCCION: CON ESTE TRABAJO AYUDAD A LOS ESTUDIANTES A CONOCER QUE ES UNA GRAFICA, LA INTERPRETACIÓN VISUAL DE DATOS ESTADISTICOAS A TRAVES DE DISTINTOS OBJETOS Y DISTINTAS PRESENTACIONES PARA REALIZAREL TRABAJO. TEMA: REPRESENTACION E INTERPRETACION DE LA INFORMACION EN LA TABLA Y GRAFICOS.
¿Para qué nos sirven los gráficos y las tablas de datos? Los gráficos y las tablas representan e interpretan información procedente de diferentes fuentes, de forma clara, precisa y ordenada. Casi todo tipos de información puede organizarse en una tabla de datos y ser representada en algún tipo de gráfico. Según las características y la cantidad de datos, conviene utilizar uno u otro gráfico. Gráficos Los más conocidos son: A- Gráficos de barras Para construir un gráfico de barras, debes dibujar un eje vertical y otro horizontal. En el espacio libre se ubican las barra. Los datos numéricos van en el eje vertical (determinando la altura de las barras) y las categorías en el eje horizontal B- Gráficos de líneas o lineal  Para construir un gráfico de barras, debes dibujar un eje vertical y otro horizontal. En el espacio libre se ubican las barra. Los datos numéricos van en el eje vertical (determinando la altura de las barras) y las categorías en el eje horizontal B- Gráficos de líneas o lineal ACTIVIDAD PARA ENTREGAR Responda las preguntas *¿Cómo interpretar los datos de una tabla de frecuencia? *¿Qué es la interpretación de gráficos estadísticos? *¿Cómo se interpretan los gráficos de barra? EVALUA ¿QUÉ APRENDÍ? ¿Cómo observa el trabajo? ¿Se te dificulto el trabajo?
¿Cómo te siente al realizar el taller asignado? ACTIVIDAD ACADÉMICA DEL ÁREA matemática DOCENTE: FECHA: SEMANA No 09 Y 10, del 09 al 20 de NOVIEMBRE NOMBRE ESTUDIANTE: _____________________________________ GRUPO:___ OBJETIVO: RECONOCER Y RELACIONAR EL METRO, COMO UNIDAD FUNDAMENTAL DE MEDIDA DE LONGITUD. INTRODUCCION:ESTE TRABAJO PERMITE UTILIZAR DIFERENTES METODOLOGIA GRAFICAS E INTERECTIVAS QUE AYUDEN A FIJAR UNAS BASES MINIMAS CON GRANDES MAGNITUDES, SIN DEJAR OTROS PROCEDIMIENTOS MÁS EXPERIMENTALES CON MAGNITUDES ACCESIBLES. MEDIDAS DE LONGITUD Las medidas de longitud se
emplean para medir la distancia existente entre dos puntos. La unidad básica es
el metro En la siguiente tabla se
muestran el nombre, la abreviatura y el valor de los múltiplos (km, hm,
dam) y submúltiplos (dm, cm, mm) más usuales
del metro. En algunos libros de Matemáticas el hectómetro se
abrevia como Hm y el decámetro como Dm. Kilómetro .-------------------Km.-----------------------1000.m Hectómetro.-----------------hm.-----------------------100.m Decámetro.------------------dam.----------------------10.m METRO.-----------------------m.-------------------------1.m Decímetro.------------------dm.------------------------0,1m Centímetro.-----------------cm.-------------------------0,01m Milímetro.-------------------mm.-----------------------0,001m Como puede observarse, el valor de cada unidad es 10 veces mayor que el inmediato inferior. Es decir: 1 km = 10 hm = 100 dam = 1.000 m = Tabla de Posición de las medidas de
Longitud
OBSERVE VIDEO: 632 medidas de
longitud.youtube.com/watch?=TlEe6yZkvCo Para convertir una unidad determinada en otra pedida, situada a su derecha (menor), tenemos que multiplicarla por la unidad seguida de tantos ceros como posiciones hay, en la tabla, entre la unidad determinada y la pedida. Recuerda que multiplicar por la unidad seguida de ceros equivale a "desplazar la coma de los decimales" hacia la derecha tantos lugares como ceros acompañan a la unidad. EJEMPLO Convertir 9 km en m. Como desde km a m hay 3 posiciones, hacia la derecha, tendremos que multiplicar por 1.000 (Los ceros a la derecha de la coma de
decimales no tienen valor y podemos poner los que necesitemos 9 ⇒ 9,00000) Para convertir una unidad determinada en otra pedida, situada a su izquierda (mayor), tenemos que dividirla por la unidad seguida de tantos ceros como posiciones hay, en la tabla, entre la unidad determinada y la pedida. Recuerda que dividir por la unidad seguida de ceros equivale a "desplazar la coma de los decimales" hacia la izquierda tantos lugares como ceros acompañan a la unidad. Convertir 120 mm en dam. Como desde mm a dam hay 4 posiciones, hacia la izquierda, tendremos que dividir por 10.000 (Los ceros a la izquierda de un número
entero no tienen valor y podemos poner los que necesitemos 120 ⇒ 00120,0).
Otras medidas de longitud Miriámetro (mam) que equivale a 10.000 metros. Año-luz, para medir grandes distancias (la que recorrería la luz en un año solar) que equivale a 9.461.000.000.000 metros. Micra, para medir distancias microscópicas, que equivale a una millonésima parte del metro ⇒ 0,000001 m. OBSERVE VIDEO: 57 Medidas de longitud para primaria.youtube.com/watch?v=aZJaaWOdS9o ACTIVIDAD: PARA ENTRGAR
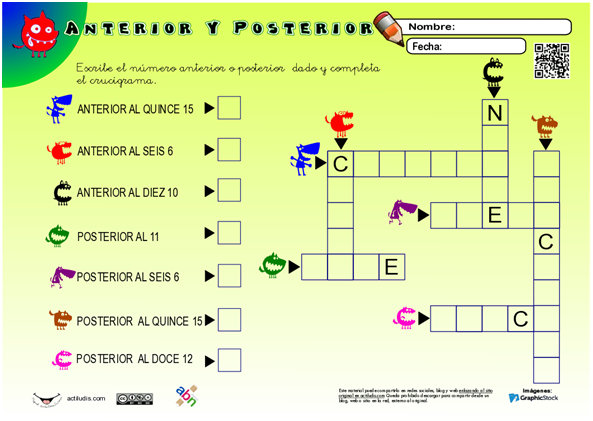
COPIAR EN EL CUADERNO. ¿QUÉ APRENDÓ? 1. ¿Cuáles son las medidas más utilizadas de longitud? 2. ¿Cuáles son las medidas de una longitud? 3. Busque el significado de otras medidas antiguas equivalente a un Metro °Alna. °Braza °Dedo °Milla °Pulgada 1. Buque el significado. A las medidas de longitud que equivale a 2.5cm °Yarda °Tonelada °Yugada 4. Responda correctamente el crucigrama. EVALUACIÓN ¿Qué Aprendí? ¿Te interesa el área de matemáticas? ¿Qué aprendiste del tema?
¿Te consideras una persona responsable al realizar la actividad?. ACTIVIDAD ACADÉMICA DEL ÁREA RECUPERACIONES MATEMÁTICA DOCENTE: FECHA: SEMANA No 11 y
12 , del 23 nov. al 04 de diciembre NOMBRE ESTUDIANTE: _____________________________________
GRUPO:____ Con ayuda de tus padres haz las siguientes actividades de
recuperación. PARA TENER EN CUENTA PRIMERO SE RESUELVEN LAS MULTIPLICACIONES
Y DIVISIONES SI LAS HAY LUEGO SE CONTINUA CON LAS SUMAS O RESTAS PARA EL
RESULTADO FINAL EJEMPLO: 4 X 5 + 3 X 6 = 20 + 18 = 38
|
GRADO 501 MATEMÁTICAS 2021
ACTIVIDAD DIAGNÓSTICA DE MATEMÁTICA
DOCENTE:
FECHA: SEMANA No 02, del 01 al 05 de febrero
NOMBRE ESTUDIANTE: ________________________________GRUPO: 5°
NOTA: Lee
las preguntas, Resuelve realizando las operaciones correspondientes y señala la opción correcta.
1. Elige la opción que dé como
resultado 85.
a) 5x8+10=
b) 10x5+15=
c) 15x4+25=
d) 20x3+35=
Observa las siguientes figuras:
2. ¿Cuántos cubos tendría la figura 4,
si tuviéramos que dibujarla?
a)
8 cubos. c) 10 cubos.
b)
9 cubos. d) 15 cubos.
3. ADIVINA. No tiene ángulos
rectos, no tiene lados paralelos,
tiene 3 vértices, todos sus ángulos son iguales. ¿De qué figura se trata?
4. Voy a comprar un lápiz en la
papelería que me cuesta $800 y un lapicero de
$1.550, ¿cuánto pagaré por ambas cosas?
a) $1.920 c)
$2.075
b) $1.025 d)
$2.350
5. Para construir una
casa, Pedro compró
20 bultos de cemento. Pagó con un cheque
de $ 300.000 ¿Cuánto le costó cada
saco de cemento?
a) $ 15.000 c)
$ 10.620
b) $ 30.000 d) $ 20.000
6. Los alumnos de 5to grado se tienen
que formar en filas de 7 para hacer una tabla
rítmica. Si el total de alumnos es de
63,
¿Cuántas
filas pueden formar?
a) 8 filas. c) 7 filas.
b) 9 filas. d) 10 filas
7. ¿Cuál es el faltante en la siguiente suma?
567+ = 777
a) 300. c) 340.
b) 210. d) 250.
8. Observa la siguiente figura y contesta.
Si con una botella se llenan 4 vasos, ¿cuántas botellas necesito
para llenar 14 vasos?
a) 4 botellas y ½.
b) 5 botellas.
c) 2 botellas y ¼.
d) 3 botellas y ½.
9. Elige el triángulo escaleno:
10. ¿Cuál de las siguientes figuras tiene mayor perímetro?
a)
Figura I. c) Figura III.
b) Figura II.
d)
Figura IV
11) Los
números primos menores
que 15 son:
a) {2, 5, 7, 9, 11,
13 }
b)
{1, 2, 3, 5, 7, 11, 13 }
c)
{1, 2, 3, 7, 9, 11, 13}
d) {2, 3, 5, 7, 11,
13 }
12) Si duermes aproximadamente 8 horas diarias.
¿Cuántas horas habrás
dormido en dos meses de 30 días?
a) 240 horas
b)
480 horas
e)
720 horas
d)
960 horas
12.
Elige la figura que tenga mayor área:
ACTIVIDAD ÁREA
DE MATEMÁTICA
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 03, del 08 al 19 de febrero
NOMBRE ESTUDIANTE: ________________________________GRUPO:
5°
OBJETIVO: Resolver problemas aditivos de cambio usando
sumas y restas.
INTRODUCCIÓN:
con este tema el niño estará en capacidad de resolver situaciones aditivas de la vida cotidiana en la que intervenga las operaciones de suma
y resta.
NOTA: con ayuda de tu familia lee la guía y resuelve los puntos dados.
Debes enviar solo la
actividad o producto a entregar a través de whatsapp o correo indicado por tu
docente.
USO
DE RELACIONES ADITIVAS EN RESOLUCIÓN DE PROBLEMAS
ACTIVIDAD
1.
En
la vida cotidiana diariamente se nos presenta situaciones en las que interfieren
las matemáticas de sumas y restas para poderlas resolver y adquirir objetos u
bienes que necesitamos.
Ahora
te invito a leer y resolver el siguiente ejercicio
Compras en el supermercado.
Juan y Patricia decidieron ir hoy a la tienda
a comprar dulces.
Para ello, Juan ha ahorrado un total
de 2500 pesos,
mientras que patricia
ahorró 1950 pesos
1. ¿Cuánto dinero tienen
ahorrado los dos para comprar
dulces?
2. ¿Qué harías para saber esto?
ACTIVIDAD 2. PROFUNDIZO
Copia en tu cuaderno.
En
la vida cotidiana diariamente se nos presenta situaciones en las que
interfieren las matemáticas; compras, devoluciones, reparticiones que requieren
ser resueltas y poder adquirir objetos u
bienes que necesitamos.
ACTIVIDAD 3. AFIANZO
Aplico los saberes que tengo sobre
resolución de problemas de suma y resta.
RESUELVE LA SIGUIENTE SITUACIÓN.
Durante el camino,
Juan se da cuenta que perdieron
un billete de 1000 pesos y no sabe dónde pudo haber sido
Imagen 3.
Dinero perdido.
1. ¿Cuánto
dinero queda de lo que tenían entre los dos
2. ¿Qué
sucede con el valor de lo que tenían ahorrado?
ACTIVIDAD 4.
PRODUCTO A ENTREGAR
A. Lee y
resuelve las preguntas de acuerdo a la situación que se presenta a
continuación.
Al llegar a
la tienda de dulces, el tendero les indica que les puede vender una bolsa de
dulces de fresa que tiene un costo de $2500 o una bolsa de chocolates que tiene
un costo de $3700
Imagen
4. Comprando dulces.
4. Si deciden comprar
los dulces de fresa ¿Cuánto
dinero les sobrará?
5. Si deciden comprar
los chocolates ¿Cuánto
dinero les hará falta?
6. ¿Cómo harías para
saber esto?
7. ¿Cuál crees que es la mejor opción
de compra? ¿Por qué?
8. ¿Qué puedes concluir de esta situación?
EVALUACIÓN Que aprendí?
Expresa con tus palabras como te sentiste o que
dificultades tú vistes al desarrollar los problemas presentados.
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 05/06, del 22 febrero
al 05 de marzo
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5° 1
OBJETIVO:
Establecer estrategias para la resolución de problemas de tipo
multiplicativo
INTRODUCCION: la vida cotidiana requiere de resolver problemas que
requieren de las matemáticas y aquí trabajaras las relaciones multiplicativas
en los números naturales.
NOTA: CON AYUDA DE TUS PADRES DESARROLLA LA GUIA.
USO DE LAS RELACIONES DE TIPO MULTIPLICATIVO.
ACTIVIDAD 1. EXPLORO
Un señor de
camino a su casa se encuentra con una nueva panadería y decide comprar 30 panes
para las 6 personas que habitan en la casa, después de realizada la compra se
dirige a su casa, pero para esto debe tomar tres buses donde cada pasaje cuesta
$1750.
Teniendo
en cuenta la información, responde las siguientes preguntas:
1.
¿Cuántos panes le corresponden a cada familiar?
¿Cómo lo SUPISTES?
2.
¿Cuánto dinero gasto en el transporte, si cada
pasaje cuesta $1750? ¿Cómo lo supiste?
Realiza las
operaciones
ACTIVIDAD 2 .
PROFUNDIZO
Copia en tu cuaderno
La multiplicación es
la suma de varios sumandos iguales o el factor total de la multiplicación de dos factores entre si ejemplo:
3 + 3 + 3 +3 =
12 ó
3 x 4= 12
Los números que se multiplican se llama factores y el resultado se
le llama producto.
La multiplicación
presenta propiedades veamos:
1.
Asociativa: Al multiplicar más de dos números
naturales, el modo en que los agrupe no altera el resultado. Por ejemplo:
2. Conmutativa: Al
multiplicar dos números naturales, el orden en qué los multiplique no altera el
resultado. Por
ejemplo:
3. Modulativa:
Multiplicar un número natural por el número 1 hace que todo número multiplicado
por él dé como resultado el mismo número.
4. Anulativa: Todo
número natural multiplicado por cero, da como resultado cero
ACTIVIDAD 3. AFIANZO
Ahora con ayuda de
tus padres vas a interpretar las situaciones. Haz las operaciones
1. Si un compañero se
transporta 35 cuadras para llegar del colegio a la casa y tú caminas tres veces
más de lo que caminó tu compañero. ¿A cuántas cuadras vives del colegio?
2. Si un empleado de
un café internet se gana 25800 pesos en un día de trabajo, y un ingeniero se
gana 8 veces esta
cantidad. ¿Cuánto se gana un ingeniero en un día de trabajo?
3. Ana María compró
un paquete de caramelos que contiene 3852 caramelos y José tiene 36 veces
esa cantidad.
¿Cuántos caramelos tiene José?
4. Escribe al frente
que tipo de propiedad es
4 x 3= 3 x 4
(4x5) x7= 7x (4x5)
4x0
345 x 1
8 x 9=9 x 8
(4x2) x10= (2x10) x4
ACTIVIDAD 4. PRODUCTO
A ENTREGAR
Desarrolla la ficha
siguiente aplicando la propiedad conmutativa y asociativa.
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 7 y 8 07/19
de marzo
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°1
OBJETIVO:
leer y escribir números de más de seis cifras.
INTRODUCCIÓN:
aprenderás la forma correcta de leer números naturales de más de seis cifras
LECTURA,
ESCRITURA Y DESCOMPOSICIÓN DE NÚMEROS DE 7 CIFRAS
ACTIVIDAD 1.
EXPLORO
DILE A UN FAMILIAR QUE TE HAGA
EL DICTADO DE CINCO NÚMEROS DE 6 O 7 CIFRAS
VER EL SIGUIENTE VIDEO https://www.youtube.com/watch?v=ex6zOUVvT28
https://www.youtube.com/watch?v=TGVvluyEfxs
ACTIVIDAD 2.
PROFUNDIZO
COPIA EN TU CUADERNO
§ Al leer números, primero se
separan las cifras, de tres en tres, empezando por la derecha. Después se leen
de izquierda a derecha, como si fuesen números de tres cifras, y se añaden las
palabras mil, millones, billones, trillones,... donde corresponda.
§ Para leer de una manera más
sencilla números grandes, acostumbramos a separar las cifras en grupos
de tres. Cuando leemos las cifras cuatro, cinco y seis, agregamos la
palabra mil. Por ejemplo:
5.243 el
número debe ser leído como “cinco mil doscientos cuarenta y
tres”.
O el
número 764.321 debe ser leído como “setecientos sesenta y cuatro mil
trescientos veintiuno”.
§ Las seis cifras siguientes
son los millones y están separadas por una comilla: ', debemos leerlas
normalmente pero agregamos la palabra millón (o millones) y después seguimos
leyendo el resto de las cifras. De esta manera el número:
9.586.545.347 debe
ser leído así: “nueve mil quinientos ochenta y seis millones quinientos
cuarenta y cinco mil trescientos cuarenta y siete”.
ACTIVIDAD 3. AFIANZO
REALIZA
LAS PÁGINAS 45,46, 49, 50 DEL TEXTO “MI
LIBRO DE TRABAJO”
ACTIVIDAD 4 . PRODUCTO A ENTREGAR
Desarrolla
las páginas de la 48, 51 y la 53 DEL TEXTO
“MI LIBRO DE TRABAJO”. Recuerda usar lápiz para desarrollar las
actividades.
ACTIVIDAD ÁREA DE MATEMÁTICA
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 09/10, del 22 al 26 de marzo
/abril 05 al 09 abril
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°
Objetivo:
Comparar números de más de siete cifras
Objetivo: aprenderás
a comparar números de más de siete cifras, determinando si es mayor, menor o
igual.
COMPARACIÓN DE NÚMEROS DE MÁS DE 7
CIFRAS
Actividad 1. Exploro
Revisa el video
https://youtu.be/PvTg5XGLpPU
Escribe en tu cuaderno como título “Comparación de
números de más de 7 cifras” y luego escribe los ejemplos que menciona el video.
Actividad 2. Profundizo
Escribe en tu cuaderno como título
“Comparación de números de más de 7 cifras”
Para comparar números de más de siete
cifras, se comparan sucesivamente las unidades de millar, las centenas de mil,
las decenas de mil, las unidades de mil, las centenas, las decenas y las
unidades
Ejemplos:
¿Cuál es mayor y cual es menor?
Primero comenzamos comparando las centenas de
millar, aquel que tenga la cifra mayor es el mayor.
|
CM |
DM |
UM |
C |
D |
U |
|
|
5 |
1 |
8 |
. |
4 |
1 |
7 |
|
2 |
1 |
6 |
. |
3 |
2 |
8 |
En este caso, el
primer número tiene 5 centenas de
millar y el segundo 2, luego el primero
es mayor.
Si los dos números tienen la misma centena de
millar, tenemos que comparar la decena de millar, aplicando el mismo
procedimiento.
Y si tuvieran la misma decena de millar, tendríamos
que comparar la unidad de millar. Y si también tuvieran la misma unidad de
millar, habría que comparar las centenas, y si también coincidieran habría que
comparar las decenas, y si también fueran iguales las unidades.
|
CM |
DM |
UM |
C |
D |
U |
|
|
8 |
2 |
1 |
. |
3 |
7 |
2 |
|
8 |
2 |
1 |
. |
3 |
7 |
1 |
Actividad 3 afianzo
En el cuaderno, ordena según se
indique.
1.
Escribe según corresponda
Ø o < o > o =
6.903.173 6.233.109
1.436.223 1.976.213
7.216.199 7.697.001
2.897.503 2.757.204
4.982.368 4.783.369
5.414.827 5.234.816
3.345.137 3.123.129
9.987.256 11.213.023
8.122.205 8.100.317
2. Lee y contesta.
●
¿Qué número es mayor 2.136.315
o
2.325.949?
●
¿Qué número es menor 5.453.010
o
5. 452.999?
●
¿Cuál de estos números
es mayor: 85.608, 85.471, 8.698?
●
¿Cuál de estos números
es menor: 6.224.363, 6.467.864, 4.234.689
Actividad
4.
Resuelve
la página 47 de “tu libro de trabajo”
GRADO
5-1
DOCENTE: YOMAIRA
AUDIVERT VALENCIA
ESTUDIANTE:
_____________________________________
PERIODO
I – SEMANA 11 y 12
ÁREAS
INTEGRADAS: tecnología, matemáticas, educación física
Guía para Aprendizaje en
Casa
|
INSTITUCIÓN
EDUCATIVA: |
I.E. La
Pastora |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
NOMBRE DEL
ESTUDIANTE: |
|
GRADO: 5º1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ÁREA/ASIGNATURA: |
1. Tecnología:
Personas que trabajan con los bienes y prestan los servicios 2. Matemáticas:
Suma y resta de números naturales (5, 6 y 7 cifras) 3. Educación
Física: Actividades coordinación (Óculo manual, óculo pie) y actividades con
pelota |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
FECHA DE
ENTREGA |
23 de abril de
2021 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
COMPETENCIAS A
DESARROLLAR: |
Conocimiento de artefactos y procesos
tecnológicos. La
formulación, el tratamiento y la resolución de problemas. Actividad motriz |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
¿INDICADORES
DE DESEMPEÑO? |
• Resuelve y
formulo problemas cuya estrategia de solución requiere de las relaciones y
propiedades de los números naturales y sus operaciones. • Realiza
formas de juego donde se trabaja el ajuste y control corporal. • Identifica
las diferentes fuentes y tipos de energía para explicar cómo se transforman. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
METODOLOGÍA: |
La guía se
desarrollará de manera virtual; se darán las explicaciones para el desarrollo
de la guía |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Principios DUA
que se contemplan
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1.
¿QUÉ
VOY A APRENDER?
La presente
guía se encuentra elaborada para ser desarrollada con los estudiantes en
compañía de un adulto. Las actividades se encuentran integradas, es decir,
que tienen 3 áreas incluidas: Tecnología, Matemáticas y Educación Física.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
TECNOLOGÍA PERSONAS QUE PRESTAN SERVICIOS O TRABAJAN CON
BIENES
Observa el
video: https://youtu.be/5ns5zI7nL5I
Escribe en tu
cuaderno como título “Personas que elaboran bienes y prestan servicios”. Escribe a qué
corresponde cada uno de los sectores económicos según el video. Si no puedes
observarlo, lee y escribe la siguiente información.
La actividad
económica se encuentra dividida en tres sectores productivos básicos según el
tipo de procesos y actividades que involucran:
El sector
primario es aquel que
abarca las actividades enfocadas en la obtención o extracción de materias
primas a partir de recursos naturales. El sector
secundario, por su
parte, es el que se encarga de procesar y transformar estas materias primas
en bienes o productos para el consumo. Es el sector industrial, caracterizado
por el uso de maquinaria. Comprende fábricas, talleres, laboratorios, así
como la industria de la construcción. El sector
terciario, por su
parte, engloba todas las actividades económicas relacionadas con los
servicios. En este sentido, no produce bienes materiales, sino que se encarga
de hacer llegar los productos elaborados por el sector secundario hasta el
consumidor. En el sector terciario, entre otras actividades, se encuentran el
comercio, las comunicaciones y los transportes.
Actividad
1. a. Completa el
siguiente cuadro agregando las personas que crees que trabajan en cada uno de
los sectores económicos y cuáles son sus funciones
EDUCACIÓN FÍSICA COORDINACIÓN
En nuestro
diario vivir ponemos a prueba constantemente nuestra coordinación física y el
equilibrio, desde subir y bajar escaleras en un centro comercial, abrir una
puerta en la oficina médica e incluso en nuestros quehaceres domésticos. Aunque parezca
algo sencillo, mantener equilibrio conlleva el esfuerzo de varios músculos
del cuerpo. Asimismo, para la coordinación debes estar alerta y utilizar
varios músculos a la vez. Entendemos la coordinación como una sucesión de
movimientos perfectamente ordenados y estructurados, que permiten un mejor
control y dominio del movimiento. La
coordinación segmentaria o específica es lo que denominamos normalmente como
coordinación óculo motriz y que solemos dividir en coordinación óculo manual (coordinación
entre ojo y mano) y coordinación óculo-pédica (coordinación entre ojo y pie).
En otras palabras, podemos decir que la coordinación segmentaria es el lazo
de unión entre el campo visual y la motricidad fina de la mano o del pie. El
objetivo fundamental de estas actividades será el desarrollar y enriquecer al
máximo las posibilidades de reacción mediante manipulaciones, lanzamientos y
recepciones de objetos con total facilidad de movimientos.
Actividad 2. a. Realiza los
siguientes ejercicios en compañía de un miembro de tu familia: - Botar
(rebotar) la pelota con las dos manos. - Lanzar la
pelota al aire y recogerla. - Rodar la
pelota por el suelo con una o dos manos. - Lanzar,
dejarla botar (rebotar) y recoger. - Por parejas
lanzarse la pelota. - Pasarse la
pelota con bote intermedio. - Botar la
pelota siguiendo el desplazamiento del compañero.
b. Observa la
imagen y sigue las instrucciones
MATEMÁTICAS SUMA Y RESTA DE NÚMEROS NATURALES (5, 6 Y 7
CIFRAS)
Dos
operaciones básicas entre los números naturales son la SUMA y la RESTA.
Al respecto,
te invito a leer y desarrollar las actividades de la página 55 de tu LIBRO DE
TRABAJO.
Cuando
realizamos sumas o restas tenemos que poner cada cifra en su columna: Escribir la
siguiente suma: 3.456.908 + 6.768.945 + 34.008 Escribir la
siguiente resta: 8.345.002 - 768.004
De esta manera,
ya ubicados los números, continuamos con la resolución de las operaciones
dadas.
ACTIVIDAD 3 a. Resuelve
las siguientes operaciones:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
PERIODO DOS
ACTIVIDAD AREA DE MATEMATICA
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 01/02 MAYO 5/21
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°1
LA FIESTA DE LOS MONSTRUOS
La realización del congreso y la fiesta fueron programadas para el mes de febrero.
Calimo quiere saber las posibilidades de que llueva precisamente el día de la fiesta.
Para eso, te pide que analices el clima de los últimos 20 febreros. Basado en esos
datos, debes analizar la posibilidad de que llueva o de que haga sol y ,a partir de
esto, debes recomendarle a los invitados traer impermeable o gafas de sol (tienes
que escribir esto en la invitación).
CLIMA EN LOS ÚLTIMOS 20 DE FEBREROS
LLUVIA/LLUVIA
sol/sol
lluvia/lluvia
lluvia/lluvia
sol/lluvia
lluvia /sol
lluvia/lluvia/
solo/sol
Al finalizar la fiesta, Calimo se entero que varios invitados tenían COVID 19,
asegurando que fue en la fiesta de cumpleaños que se contagiaron. …
Calimo comenzó a realizar un rastreo para identificar quien origino los contagios.
Después de finalizar las llamadas, se dio cuenta que 5 monstruos habían asistido
con síntomas a la fiesta, sin saber que tenían COVID-19
Una persona con COVID 19, puede contagiar a 3 persona mas…
Teniendo en cuenta esta información…
¿A cuantas personas pudieron haber contagiado las 5 personas que tenían
COVID?
Si el tapabocas se debe cambiar cada 3 horas ¿Cuántos tapabocas se deben
comprar en 8 días para cada persona que se encuentre infectada?
Si la mitad de las personas contagiadas se agravan y necesitan una UCI ¿Cuántas
camas de UCI se necesitan para atenderlos?
El alcalde de Medellín, Daniel Quintero, informó que la ciudad llegó a 1.031 camas
de Unidades de Cuidados Intensivos (UCI) activas; sin embargo, los contagios
hacienden a 1.401, de los cuales 988 están en hospitalización general
¿Cuántas personas se encuentran esperando una cama UCI?
Si en Medellín, se infectan 230 personas al día..
¿Cuántas personas se podrían morir por no encontrar una UCI en Medellin?
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 03/04 mayo 24
al 07 junio
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°1
MULTIPLICACION Y DIVISIÓN
1. EXPLORACIÓN
https://www.youtube.com/watch?v=4qdOjfmJVR8
Escribe en tu cuaderno como
título “Multiplicación de números naturales” y luego escribe las
multiplicaciones del video en tu cuaderno, y resuélvelas.
https://www.youtube.com/watch?v=CGahpaqdA5U, aquí encontrarás una breve explicación de la división usando restas y partiendo del reparto. Mira también este video donde la resta se realiza mentalmente
https://www.youtube.com/watch?v=wuY3_oC_3CM.
Escribe en tu cuaderno como
título “División de números naturales” y luego escribe las divisiones del video
en tu cuaderno, y resuélvelas.
Nota: Quienes no puedan
acceder al enlace realizar las siguientes
123x21=
233x23=
división
9687: 23
1456:56
2. PROFUNDIZO
Leo el proceso para
multiplicar números por dos o tres
cifras.
Pasos para hacer una multiplicación de 2 y de 3 cifras
1. Multiplicar las unidades del multiplicador
por el multiplicando y el resultado escribirlo en la fila de abajo.
2. Multiplicar las decenas del multiplicador
por el multiplicando y el resultado escribirlo en la fila de abajo pero
desplazado una posición a la izquierda.
3. Sumar los productos.
Como vemos en la imagen sumamos los productos y el
resultado de la multiplicación es 74.195
DIVIDIR:
Tomamos las dos primeras cifra de la izquierda del
dividendo (57).
Importante: las dos
cifras tomadas (57) tienen que ser igual o mayor que el divisor (36). Si fueran
menor tomaríamos tres cifras (578).
Si dividiéramos por 3 cifras tomaríamos las 3
primeras cifras del dividendo, siempre y cuando fueran igual o mayor que el
divisor.
Por ejemplo: 34.679 : 256 tomaríamos 346
Si las tres primeras cifras fueran menor que el
divisor habría que tomar 4 cifras.
Por ejemplo: 14.679 : 256 tomaríamos 1467
Seguimos: buscamos el número que multiplicado por
36 se aproxime más a 57 sin pasarse. Ese número es 1, porque 1 x 36 = 36 (es el
que más se aproxima a 57 sin pasarse). El 2 no nos valdría porque 2 x 36 = 72
(se pasa)
¿Cómo encuentro ese número?
Nos centramos en 57 y 36, y en concreto en sus dos
primeras cifras 5 y 3, busco el número de la tabla del 3 que más se aproxime a
5 y ese número es 1.
Pero atención: imagina que estamos dividiendo 67.842 entre 36. Tomamos sus dos
primeras cifras 67 y 36, y en concreto nos centramos en el 6 y en el 3.
¿Qué numero de la tabla del
3 se aproxima más a 6 sin pasarse? el 2.
¿Tomaríamos el 2? No, porque 36 x 2 = 72, mayor que
67, por lo que no nos vale, tendríamos que coger un número menor (el 1).
Sigamos: multiplicamos 1 x 36 y se lo restamos a
57.
Bajamos la siguiente cifra (8).
Volvemos a realizar el mismo proceso. Buscamos el
número que multiplicado por 36 más se aproxime a 218 sin pasarse. Ese número es
6, porque 6 x 36 = 216 (es el que más se aproxima a 218 sin pasarse).
Multiplicamos 6 x 36 y se lo restamos a 218.
Bajamos la siguiente cifra (4).
Tenemos ahora un problema: 24 es menor que 36 luego
no lo puedo dividir. ¿Qué hacemos?
Ponemos un 0 en el cociente.
Y bajamos la cifra siguiente (2):
Seguimos dividiendo: buscamos el número que
multiplicado por 36 más se aproxime a 242 sin pasarse. Ese número es 6, porque
6 x 36 = 216 (es el que más se aproxima a 242 sin pasarse).
Multiplicamos 6 x 36 y se lo restamos a 242.
Como ya no hay más cifras del dividendo que bajar
la división ha finalizado.
El cociente es 1606 y el resto es 26.
3. Afianzo
Realiza las siguientes
actividades de multiplicación, revísalas y luego escríbelas en el cuaderno.
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/mult-num-2-cifras
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/mult-num-2-cifras-2
Nota: Quienes no puedan
acceder al enlace realizar las siguientes multiplicaciones en el cuaderno.
Realiza las siguientes
actividades de división, revísalas y luego escríbelas en el cuaderno.
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/terminos-divisiones-1
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/terminos-divisiones-2
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/prueba-division
Nota: Quienes no puedan
acceder al enlace realizar las siguientes DIVISIONES en el cuaderno.
ACTIVIDAD 4. EJERCITACIÓN
Resuelve las operaciones de
la página 56, 60 de tu libro de trabajo. Ten en cuenta que cuando aparecen los
: (dos puntos), significa que es dividido; es decir, 432:2 es 432 dividido 2.
ACTIVIDAD ACADÉMICA DEL
ÁREA DE MATEMATICA
DOCENTE: |Yomaira audivert
FECHA: SEMANA No 05/06 JUNIO DEL 7 AL 18
NOMBRE
ESTUDIANTE: _____________________________________ GRUPO: 5°1
POTENCIACIÓN
ACTIVIDAD 1
1.1. EXPLICACIÓN
En tu
cuaderno escribe la siguiente información
La potenciación
Las potencias son una manera abreviada de escribir
una multiplicación formada por varios números iguales. Son muy útiles para
simplificar multiplicaciones donde se repite el mismo número.
Las
potencias están formadas por la
base y por el exponente. La base es el número que se está multiplicando
varias veces y el exponente es el número de veces que se multiplica la base.
¿Qué es la base?
Es
el número que se está multiplicando.
¿Qué es el exponente?
Las
veces que se repite el número.
¿Cómo se forma una potencia?
Se
disponen de la siguiente manera: el número de la base de escribe de forma
normal, y el número de la potencia se escribe más pequeño que la base en la
parte superior derecha.
Vamos a verlo con el siguiente ejemplo:
5 x
5 x 5 x 5 x 5 x 5 x 5
·
¿Qué
número se está multiplicando? El 5, por lo tanto, es la BASE
·
¿Cuántas
veces se repite el número? 7 veces, por lo tanto, es el EXPONENTE
Escribiendo
la potencia quedaría así:
Vamos a ver otro ejemplo: 3 x 3 x 3 x 3
·
¿Qué
número se está multiplicando? El 3, por lo tanto, es la BASE
·
¿Cuántas
veces se repite el número? El número se repite 4 veces, por lo tanto, es el
EXPONENTE
3 x
3 x 3 x 3 = 3 4
ACTIVIDAD 2. AFIANZAMIENTO
Resuelve las siguientes
potencias para ir practicando.
ACTIVIDAD 3. EJERCITACIÓN
PARA ENTREGAR
Resuelve las páginas 64,
65, 66 y 67 de tu libro de trabajo
TEMA 2 . RADICACIÓN
ACTIVIDAD 1. EXPLICACIÓN
En tu
cuaderno escribe la siguiente información
La radicación
La radicación es la operación inversa de la
potenciación; es decir si nos dan el área de un cuadrado, extraer la raíz es
encontrar el lado de ese cuadrado; mientras que en la potenciación nos dan el
lado del cuadrado y encontramos el área.
Supongamos que nos dan un número y nos piden
calcular otro, tal que, multiplicado por sí mismo un número de veces nos da el
número.
Por ejemplo: calcular qué número multiplicado por sí
mismo 2 veces da 196. Ese número es 14. Porque 14 x 14 = 196 → √196
= 14
El número que está dentro del radical se
llama radicando, el grado de la raíz se llama índice y
se encuentra en la V del radical, el resultado se llama raíz.
La mejor forma de encontrar las raíces de cualquier
número exacto es convertir las raíces a potencias en donde la base de la
potenciación es la raíz buscada.
Las raíces se llaman según su índice, así:
Para el índice 2 (si el índice es 2, se suele
omitir) se le llama raíz cuadrada.
Para índice 3, se llama raíz cúbica; – índice
4, raíz cuarta; – índice 5, raíz quinta, y así sucesivamente, es decir se
nombra el número ordinal.
ACTIVIDAD 2. AFIANZAMIENTO
Resuelve
las siguientes raíces para ir practicando.
ACTIVIDAD 3. EJERCITACIÓN
PARA ENTREGAR
Resuelve
las páginas los puntos 1, 2, 3 y 8 de las páginas 74 y 75 en tu libro de
trabajo.
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 07/08 julio 12 /23
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°1
LOGARITMACIÓN
ACTIVIDAD 1. EXPLICACIÓN
Se llaman logaritmo a la potencia que se tiene que
elevar en otro número y es llamado base del sistema, se trata en términos
generales de un número positivo sirve para obtener el mismo número. Esto es que
el logaritmo es el opuesto a la potenciación donde el logaritmo es la potencia.
Obtenemos tres términos que se llaman:
- Base del logaritmo
- Número del logaritmo
- Logaritmo
Así en una potencia:
El cinco se eleva al cuadrado y se obtiene el número
25
Aquí en esta potenciación al pasarla a logaritmo
obtenemos lo siguiente:
La base de potencia ahora es la Base del logaritmo =
5
La potencia ahora es el Número del logaritmo = 25
El exponente ahora es el Logaritmo = 2 el cual se
coloca en subíndice
Ahora la forma en la que se lee el logaritmo es de
la siguiente manera:
Se lee Logaritmo en base 5 de 25 = 2
ACTIVIDAD 2. AFIANZAMIENTO
Resuelve
los siguientes ejercicios para ir practicando.
ACTIVIDAD 3. EJERCITACIÓN
( PARA ENTREGAR)
A.
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 09/10 julio 26 /AGOSTO 06
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°1
1-
MÍNIMO COMÚN MÚLTIPLO
ACTIVIDAD 1.
Para ir
introduciendo el tema, mira con atención el siguiente vídeo.
ACTIVIDAD 2.
En tu
cuaderno escribe la siguiente información
El mínimo común múltiplo de dos
números a y b es el número más pequeño que es
múltiplo de a y múltiplo de b.
Para denotar
el mínimo común múltiplo de a y b escribiremos m.c.m.(a, b) ó mcm(a, b).
Ejemplo:
Vamos a
calcular el mínimo común múltiplo de 4 y 6. Para ello, escribimos los primeros
múltiplos de 4 y de 6:
Recordad que
los múltiplos se obtienen multiplicando.
Entre los 6
primeros múltiplos de 4 y de 6, los números 12 y 24 son múltiplos de ambos
(son múltiplos comunes).
Tenemos que
quedarnos con el mínimo.
Por tanto,
el mínimo común múltiplo de
4 y 6 es 12:
m. c. m (4,6) = 12
En un
problema sería así:
ACTIVIDAD 3.
Afianzamiento
Practica lo
aprendido en los siguientes links
ACTIVIDAD 4.
Ejercitación
Resuelve las
páginas 79 y 80 en tu libro de trabajo.
MÁXIMO COMÚN
DIVISOR
ACTIVIDAD 1.
EXPLORACIÓN
Para ir
introduciendo el tema, mira con atención el siguiente vídeo.
ACTIVIDAD 2
En tu
cuaderno escribe la siguiente información
Los divisores de un número
Los
divisores de un número natural son los números naturales que lo pueden dividir,
resultando de cociente otro número natural y de resto 0.
Ser divisor
es lo recíproco a ser múltiplo. Si 9 es múltiplo de 3, entonces 3 es divisor de
9.
Los
divisores de un número natural le pueden dividir, su división es exacta.
Cada número
tiene una cantidad concreta de divisores. El número 1 tiene sólo un divisor, él
mismo.
Solamente el
0 tiene infinito número de divisores, ya que todos los números son divisores de
0.
Por ejemplo:
D12=
{1,2,3,4,6,12}
D30=
{1,2,3,5,6,10,15,30}
D8=
{1,2,4,8}
En un
problema sería lo siguiente:
ACTIVIDAD 3.
Afianzamiento
Práctica lo
aprendido en los siguientes links
http://ntic.educacion.es/w3//recursos/primaria/matematicas/conmates/actividades/jbc21.htm
ACTIVIDAD 4.
Ejercitación
Resuelve las
páginas 70 y 71 de tu libro de trabajo.
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 11/12 AGOSTO 09/20
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°1
NÚMEROS
PRIMOS Y COMPUESTOS
ACTIVIDAD 1. INTRODUCCIÓN
Para ir introduciendo el tema,
mira con atención el siguiente vídeo.
ACTIVIDAD 2. PROFUNDIZO
En tu cuaderno escribe la
siguiente información:
NÚMEROS
PRIMOS Y COMPUESTOS
Los números
primos son aquellos que solo, muy importante, solo son divisibles (al
dividirse entre otro da un número entero) entre ellos mismos y el 1.
Por
ejemplo: el 7 es un número primo porque solo es divisible por 7 y por 1. Otro
ejemplo, el 13 es un número primo porque solo lo podemos dividir entre 1 y 13.
Además, se puede escribir como la multiplicación de 1×13, pero no como otra
multiplicación de números naturales.
Los
números compuestos son aquellos que
son divisibles por ellos mismos, por la unidad y también por otros números.
Recuerda, el número 1 no se considera ni compuesto ni primo por convenio.
El
25 es un número compuesto. Entonces es divisible por 1, por 25 y por 5. Es
decir, 25/25= 1, 25/1= 25 y 25/5=5.
El
14 es un número compuesto y no es primo. Es divisible por 1, por 2, por 7 y por
14. Lo comprobamos: 14/1 = 14, 14/2 = 7, 14/7 = 2 y 14/14 = 1.
Estos
son los números primos hasta el 1.000
10.2. Afianzamiento
Resuelve
los siguientes ejercicios para ir practicando. No debes escribir nada en tu
cuaderno.
ACTIVIDAD
3. Ejercitación
Resuelve
la siguiente actividad en tu cuaderno
LOS POLÍGONOS
ACTIVIDAD
1. EXPLORO
Revisa los
siguientes vídeos
ACTIVIDAD 2.
PROFUNDIZO
1- Escribe en tu cuaderno la siguiente información:
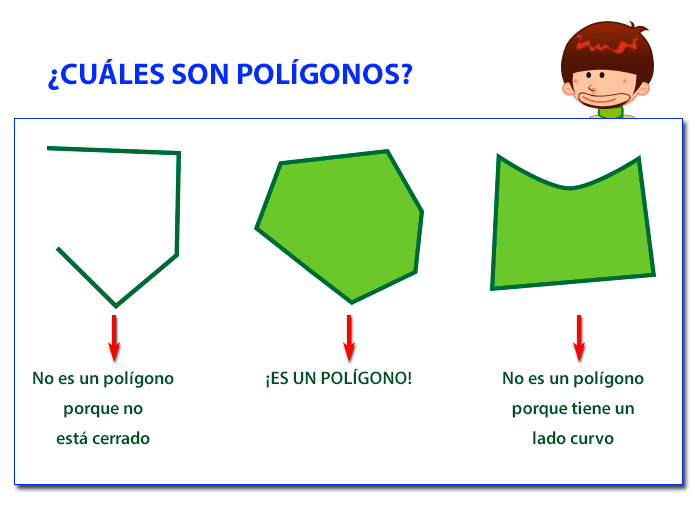
Un polígono es
el área de un plano que está delimitado por líneas que tienen que ser rectas.
Si hacemos caso a
la etimología de la palabra, polígono proviene de los términos griegos «poli»
y «gono«. «Poli» podría traducirse como «muchos» y «gono»
como «ángulo». Atendiendo a esto podríamos decir que un polígono es
literalmente aquello que tiene muchos ángulos.
Para considerar
polígono a una figura esta debe cumplir que sus líneas siempre deben ser rectas
y que no puede estar abierto. En la siguiente imagen puedes ver varios ejemplos
de polígonos y otros que no lo son:
2- Luego lee la información que se encuentra en la página 132 en la sección
Debes aprender... Luego dibuja los siguientes polígonos regulares e irregulares.
ACTIVIDAD 3. AFIANZO
Realiza la
siguiente actividad para practicar. No debes escribir nada en el cuaderno.
ACTIVIDAD 4. Ejercitación
Resuelve la
página 132 de tu libro de trabajo.
CLASIFICACIÓN DE LOS POLÍGONOS (GEOMETRÍA)
ACTIVIDAD 1. EXPLORO
Revisa el siguiente vídeo: https://youtu.be/fobhsYGab40
ACTIVIDAD 2. PROFUNDIZO
Escribe en tu cuaderno la siguiente
información:
Clasificación de polígonos
Podemos clasificar los polígonos de tres
formas diferentes:
- Clasificación
de polígonos según sus lados:
- Triángulo: 3 lados
- Cuadrilátero: 4 lados
- Pentágono: 5 lados
- Hexágono: 6 lados
- Heptágono: 7 lados
- Octógono: 8 lados
- Eneágono: 9 lados
- Decágono: 10 lados
- Endecágono: 11 lados
- Dodecágono: 12 lados
- Clasificación
de polígonos según sus ángulos:
- Polígonos
cóncavos:
es cuando el polígono tiene un ángulo que mide más de 180º.
- Polígonos
convexos:
es cuando todos los ángulos del polígono miden menos de 180º.
- Clasificación
de polígonos según sus lados y sus ángulos:
- Polígonos
regulares:
es cuando un polígono tiene todos sus lados y ángulos iguales.
- Polígonos
irregulares:
es cuando en un polígono hay uno o más lados y/o ángulos que no son
iguales.
ACTIVIDAD 3. Afianzamiento
Realiza las siguientes actividades para
practicar. No debes escribir nada en el cuaderno.
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/juego-identificacion-figuras
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/juego-vertices-y-angulos
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/juego-poligonos-regulares
ACTIVIDAD 4. Ejercitación
Resuelve las páginas 133 y 134 de tu
libro de trabajo.
ACTIVIDAD AREA DE
MATEMÁTICA
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 13 AGOSTO 23 /SEP 03
NOMBRE ESTUDIANTE:
________________________________GRUPO: 5°1
POLÍGONOS
CÓNCAVOS Y CONVEXOS (GEOMETRÍA)
11.1.
Explicación
Revisa el siguiente
video: https://youtu.be/3C80v0Qg-n0
Escribe en tu cuaderno
la siguiente información que encuentras en la página 135 de tu libro de trabajo
en la parte “DEBES APRENDER”.
11.2.
Afianzamiento
Realiza las siguientes
actividades para practicar. No debes escribir nada en el cuaderno.
A. Resuelve:
B. Explora las
páginas:
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/juego-concavos-y-convexos
11.3. Ejercitación
Resuelve las páginas
135 y 136 de tu libro de trabajo.
 ACTIVIDAD
AREA DE MATEMÁTICA
ACTIVIDAD
AREA DE MATEMÁTICA
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No. 13 AGOSTO 23 /SEP 03
NOMBRE ESTUDIANTE: ________________________________GRUPO:
5°1
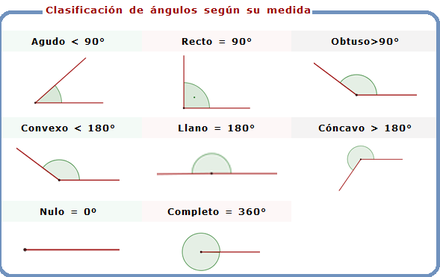
Tipos de ángulos
1. EXPLORO
Revisa el vídeo https://www.youtube.com/watch?v=6wscEyBlPLA
presta mucha atención a la explicación.
2. PROFUNDIZO
Escribe en tu cuaderno como
título “Tipos de ángulos” y luego escribe la siguiente información en tu
cuaderno https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/clasificacion-de-angulos.html
- tema_clasificacion-de-angulos-segun-su-medida
Realiza las siguientes
actividades de clasificación de ángulos
4. Ejercitación
Resuelve las operaciones de las
páginas 121 y 122 de tu libro de trabajo.
 ACTIVIDAD AREA REFUERZO DE MATEMÁTICA
ACTIVIDAD AREA REFUERZO DE MATEMÁTICA
DOCENTE: YOMAIRA AUDIVERT
FECHA: SEMANA No 13 AGOSTO 23 /SEP 03
NOMBRE ESTUDIANTE:
________________________________GRUPO: 5°1
DESARROLLA LAS SIGUIENTES ACTIVIDADES:
BUSCA EL MINIMO COMUN MULTIPLO DE LOS SIGUIENTES NÚMEROS.DOCENTE:
YOMAIRA AUDIVERT
FECHA:
SEMANA No 01/ 02 FECHA: SEPTIEMBRE 06/
17
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°1
ACTIVIDAD
1. CONCEPTO DE FRACCIÓN
1.1.
EXPLICACIÓN
Para ir introduciendo
el tema, mira con atención los siguientes videos
https://youtu.be/c9cTIjBqFTw
En tu cuaderno escribe
la siguiente información
¿QUÉ ES UNA FRACCIÓN?
Definición
Una fracción es un
número, que se obtiene de dividir un entero en partes iguales. Por ejemplo,
cuando decimos una cuarta parte de la torta, estamos dividiendo la torta en
cuatro partes y consideramos una de ellas.
Una fracción se
representa matemáticamente por números que están escritos uno sobre otro y que
se hallan separados por una línea recta horizontal llamada raya
fraccionaria.
La fracción está
formada por dos términos: el numerador y el denominador. El numerador es el número que está sobre la raya fraccionaria y el denominador
es el que está bajo la raya fraccionaria.
El NUMERADOR es el número de partes que se considera de la unidad o total.
El DENOMINADOR es el número de partes iguales en que se ha dividido la unidad
o total.
Lectura
de fracciones
Todas las fracciones
reciben un nombre específico, se pueden leer como tal, de acuerdo con el
numerador y denominador que tengan.
El número que está en
el numerador se lee igual, no así el denominador. Cuando el denominador va
de 2 a 10, tiene un nombre específico (si es 2 es "medios", si es 3
es "tercios", si es 4 es "cuartos", si es 5 es
"quintos", si es 6 es "sextos", si es 7 es
"séptimos", si es 8 es "octavos", si es 9 es
"novenos", si es 10 es "décimos"), sin embargo, cuando es
mayor que 10 se le agrega al número la terminación "avos".
Ejemplos:
En
el caso particular de las fracciones con denominador 10, 100 y 1000.
Ejemplo: 4 se lee
"cuatro décimos", 2 se lee "dos centésimos" y
3 se lee "tres milésimos"
1.2.
AFIANZAMIENTO
Practica lo aprendido:
a. Desarrolla en tu
cuaderno y colorea atendiendo a la explicación anterior
b. Desarrolla en el
cuaderno dibujando y escribiendo el fraccionario que representa cada figura.
1.3.
EJERCITACIÓN
Resuelve la página 86
en tu libro de trabajo.
DOCENTE:
YOMAIRA AUDIVERT
FECHA:
SEMANA No 01/ 02 FECHA: SEPTIEMBRE 06/
17
NOMBRE
ESTUDIANTE: ________________________________GRUPO: 5°1
ACTIVIDAD
2. FRACCIÓN DE UN NÚMERO
2.1.
EXPLICACIÓN
Para ir introduciendo
el tema, mira con atención el siguiente video.
https://youtu.be/ZNgpSrNEU8E
En tu cuaderno escribe
la siguiente información
FRACCIÓN DE UNA CANTIDAD
Para calcular la
fracción de una cantidad, se divide la cantidad por el denominador de la
fracción y el resultado se multiplica por el numerador.
Ejemplo:
3/6 de
60——————-> 3/6 x 60 = (60/6) x3 =10 x 3 = 30
2/4 de 360
————-> 2/4 x 360 = (360/ 4) x 2 = 90 x 2 = 180
Observa la fracción
que se indica en cada caso
1/4 de 12 = (12/4)
x1 3/4 de
16= (16 /4) x3 1/9 de
18 = (18/9) x 1
= 3 x
1
= 4 x
3
= 2
x 1
=
3
=
12 = 2
Las estrellas
coloreadas Los triángulos azules Corazones
coloreados de rojo
2.2.
AFIANZAMIENTO
Practica lo aprendido
en los siguientes links
http://ntic.educacion.es/w3//recursos/primaria/matematicas/conmates/actividades/jbc21.htm
Practica
lo aprendido
Ejercita tu mente y
pon a prueba tus conocimientos
1. Colorea la fracción
que se indica en cada caso y haz la operación
3/5 de
15
3/6 de 24
1/3 de 21
2. Calcula la fracción
de cada cantidad, empleando la multiplicación y la división.
Sigue el ejemplo
a) 3/5 de
80= 3/5 x 80= 3 x 80
/5= 240 / 5= 48
b)
9/4 de 52 = ————— = —————- = ————- = ———-
c)
10/3 de 60= ————— = —————- = ————- =
———-
d)
2/5 de 5 = ————— = —————- = ————- =
———-
3. Selecciona la
respuesta correcta encerrándola en un círculo en cada una de las siguientes
situaciones.
a) Para descansar bien
se recomienda dormir la tercera parte del día. ¿Cuántas horas se deben dormir
diariamente?
16
horas
8
horas
10 horas
b) Si Ernesto hace
deporte 5/7 de los días de una semana. ¿Cuántos días de la semana hace deporte?
5 días
2 días
7 días
c) Ana María
compró 25 paquetes de galletas para consumir en la semana. Si al
final de la semana supo que había consumido 3/5 de ellas. ¿Cuántos paquetes de
galletas consumió?
10
paquetes 15
paquetes
20 paquetes
4. Resuelve: Lee
interpreta y soluciona
a) Pablo caminó de la casa al colegio 5/12 de hora. ¿Durante cuantos minutos
caminó Pablo?
b) Pedro cortó 2/5 de una cuerda de alambre de 200 cm. de longitud.
¿Cuánto miden ahora las dos partes de cuerda?
c) En una granja hay 180 gallinas. Si 3/6 de ellas pusieron huevos.
¿Cuántas gallinas aun faltan por poner?
2.3.
EJERCITACIÓN
Resuelve la página 90
de tu libro de trabajo.








































































































No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.